Non-convex polyhedra are the opposite of convex polyhedra. This means that non-convex polyhedra (or concave polyhedra) are more or less star shaped. If you connect a string between two vertexes of a solid than it is possible this string is running through the air.

Non-convex polyhedra are often beautiful solids. At first they seems to be quite complicated but if you deep further into this material you will see that there is a overlap with the convex polyhedra.

A few puzzles are even based upon non-convex polyhedra. 

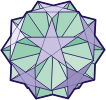
	Kepler-Poinsot Polyhedra You will find here the four Kepler-Poinsot polyhedra: the Great dodecahedron, the great icosahedron and then great and small star dodecahedron.
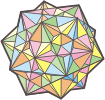
	Uniform polyhedra Uniform polyhedra are all those polyhedra who are formed by regular polygons, are half-regular, but not convex. A total of 85 has been described.
	Compound polyhedra By combining two or more polyhedra to one solid, you can get the most extraordinary and beautiful polyhedra. In this chapter you will find some examples of these 'compound polyhedra'
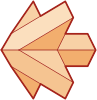
	Stellations Stellating is the process of making the faces of a polyhedron longer, so it will become a star. In some polyhedra this is not possible, but in others you can get marvelous stars.
	Previous menu Click here to return to the main menu