Design by Peter Query

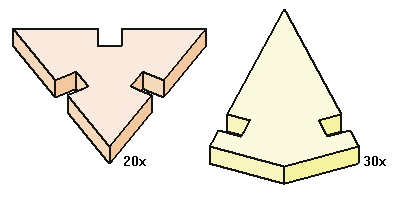
Ico is based upon an icosahedron. An icosahedron is made out of twenty triangles, has twelve corners and thirty edges. This puzzle uses the same type of connections as the Dodec puzzle. To make this puzzle you have to saw twenty triangles and thirty kite shapes.

You can make the Ico puzzle, by sawing the pieces according to the diagram below. Use the design graph for the exact values. Just as by the Dodec puzzle you can use wood of a thickness of 1 to 1,5 cm. After that you can simply connect the pieces together using the picture above as an example.

In the diagram above every notch has an equal depth, namely exact the thickness of the wooden plate. A variant to this is to use pieces with notches of different depths. If you use wood of a thickness of 10 units, the different notches will be 5, 10 or 15 units deep. One piece can have notches of different depths. For triangles you can make ten different combinations of notches, the kite shapes have six different combinations. All different pieces are shown in the picture below.

From the pieces above you can choose twenty triangles and thirty kite shapes which can make an Ico puzzle. There are a lot of combinations possible to form a complete puzzle. An example of such a combination is to take all triangles twice, kite shape 1-3 twenty times and kit shape 2-2 ten times. The solution for this example is not difficult to find. The question remains which combination of triangles and kite shapes will give the fewest solutions and therefore the most difficult puzzle.