Niet convexe veelvlakken zijn het tegenovergestelde van convexe veelvlakken. Dit betekend dat niet convexe veelvlakken (of concave veelvlakken) meer of minder stervormig zijn. Als je twee hoekpunten van een niet-convex veelvlak met een draad verbind, dan kan deze draad door de lucht lopen. 

Niet-convexe veelvlakken zijn vaak mooie figuren. Op het eerste gezicht lijken ze erg complex, maar als je dieper op dit materiaal ingaat, dan zul je merken dat er een duidelijke overlap bestaat met de conventionele convexe veelvlakken,

Een paar puzzels zijn zelfs gebaseerd op niet-convexe veelvlakken.

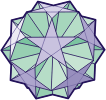
	Kepler-Poinsot Veelvlakken Hier vind je de vier Kepler-Poinsot veelvlakken: de grote en kleine sterdodecaëder, de grote dodecaëder en grote icosaëder. Ook worden twee 'rhombische Kepler-Poinsot veelvlakken' besproken
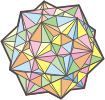
	Uniforme veelvlakken Uniforme veelvlakken zijn alle veelvakken die gevormd worden door regelmatige veelhoeken, die half regelmatig zijn, maar niet convex. In het totaal zijn 85 van dit soort veelvlakken beschreven en deze worden onder de naam 'uniforme veelvlakken' verzameld.
	Samengestelde veelvlakken Door twee of meer veelvlakken te combineren, dan kan je de meest bijzondere en mooie veelvlakken creëren. In dit hoofdstuk kun je een aantal voorbeelden van 'samengestelde veelvlakken' terugvinden.
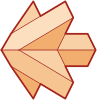
	Versterring Versterring is het proces, waarbij de zijden van een veelvlak langer gemaakt worden om zo een ster figuur te creëren. Bij sommige veelvlakken si dit helemaal niet mogelijk, maar bij andere kunnen zo bijzondere sterfiguren ontstaan.

Vorig menu Klik hiernaast om terug te keren naar het hoofdmenu.