Regularity is an important concept in polyhedra. Well known are the 'regular' or 'Platonic' polyhedra which are considered as completely regular. Archimedic and Catalan polyhedra are half-regular polyhedra. 

Now is the question how regularity is determined. Who or what defines which polyhedron is regular and which not. For answering of this question the following five rules are frequently used. If all five rules are applicable to a polyhedron, than that polyhedron is completely regular. 

1. The faces are regular polyhedrons

2. The faces are congruent (identical in shape)

3. The vertexes are congruent

4. The dihedral angles are congruent

5. The polyhedron is convex

The Platonic polyhedra apply to all these five rules and are thus completely regular. Archimedic polyhedra apply to rules 1, 3 and 5 and are therefore half-regular. The cuboctahedron and icosidodecahedron also apply to rule number 4 (but remains half-regular). Catalan polyhedra apply to rules 2, 4 and 5. The rhombic polyhedra apply to rules 2, 3, 4 and 5. Catalan and rhombic polyhedra are therefore also half-regular. 

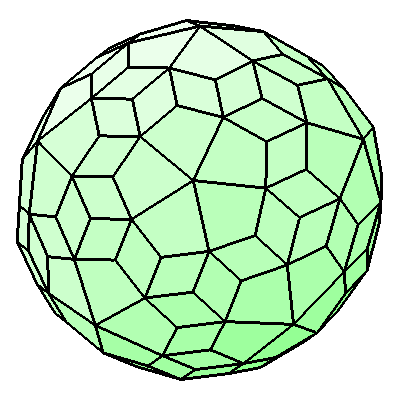
The five rules are quite limited to determine how regular a polyhedron is. For example the polyhedron shown below: a rhombic deltoïd pentacontahectahedron. This polyhedron is completely irregular according to the rules above: the faces are no regular polyhedra, the faces are not equal, the vertexes are not congruent, and the dihedral angles also differs. The only thing you can say is that the polyhedron is convex. However, this polyhedron seems to have some kind of 'regularity'

To gain more insight in the exact regularity of a polyhedron, I would like to introduce the concept 'regularity index'. This index is a relation between the number of edges of a polyhedron (as a size for its dimension) and the number of repetitions within the polyhedron. More information about this regularity index can be found on the next tab.