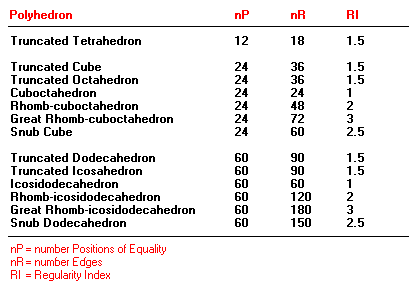
First I would like to demonstrate the use of the regularity index in the half-regular polyhedra: the Archimedic and Catalan Solids. The number of positions of equality is quite easy to determine. These are equal to the corresponding Platonic solid. For example, a truncated tetrahedron has twelve positions of equality, while a truncated cube or octahedron has 24 .

The number of edges of an Archimedic or Catalan polyhedron is however variable, therefore are not al regularity indexes the same (although they are all 'half-regular polyhedra'). In the table below a summary is given off the different Archimedic solids with their corresponding regularity indexes. 

The value of the regularity index is between 1 and 3 in Archimedic solids. This means that not all Archimedic polyhedra do have the same regularity. The regularity index is thus much more precise in determining how regular a polyhedron is than the five rules described before. Remarkable is that truncating a polyhedron will increase the regularity index threefold (In fact a great rhomb-cuboctahedron is a truncated version of the cuboctahdron, and this observation applies also to these solids).

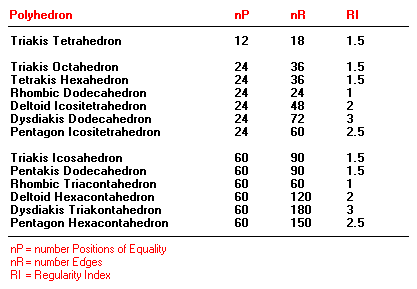
The Catalan polyhedra are the dual counterparts of the Archimedic solids. You can expect that the regularity index is the same as in the Archimedic polyhedra. You can check by yourself that this is correct. In the table below a summary regarding the regularity index in Catalan solids is given. 

If you calculate the regularity index of other (half-regular) polyhedra, than you can find out that the RI in prisms is 1.5, in anti-prisms 2, in double pyramids 1.5 and in trapezoids 2. 

Below another example for calculating the regularity index. All three polyhedra do have 12 edges. All three polyhedra aplies to at least three of the five rules of regularity (solids are convex, vertexes are congruent and dihedral angles are congruent). The first polyhedron is a cube with a regularity index of 0.5. The second solid has 8 positions of equality and therefore a regularity index of 1.5. The last polyhedron has a regularity index of 3, because the number of positions of equality is only 4. 

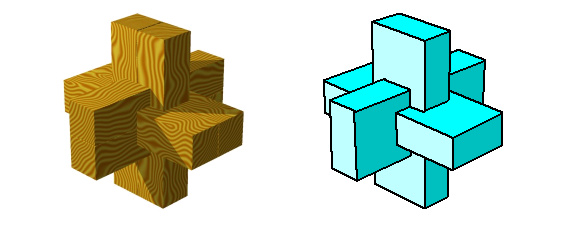
It is possible to calculate the regularity index of non-convex polyhedra. It will be shown that the regularity index of Kepler-Poinsot polyhedra is 0.5, just like the Platonic solids. Also puzzles, which are often non-convex in shape, do have a regularity index. For example the Chinese Cross Puzzle. This puzzle can be seen as a compound of three square beams. In total this 'polyhedron' has 36 edges. The number of positions of equality is 12. De regularity index of a Chinese Cross Puzzle is 3 and could therefore been seen as 'half-regular'. 

The last example is the rhomb-deltoid-pentacontahectahedron already mentioned at the 'five rules' of regularity. This polyhedron has 300 edges. The number of equality is 60 (so quite high). De regularity index is 5. So not very more irregular than for instance Archimedic polyhedra....