Pentomino's zijn de twaalf stukken van een bekende puzzel. Van oorsprong is deze puzzel plat. De twaalf stukken zijn alle mogelijkheden waarop vijf vierkanten met elkaar gecombineerd kunnen worden. Er bestaan of domino's (twee vierkanten), triömino's (drie vierkanten, in het totaal twee verschillende mogelijkheden), tetraömino's (vier vierkanten, vijf mogelijkheden, zoals in het computerspel Tetris) en hexomino's (zes vierkanten, 35 mogelijkheden). De pentomino's bestaan in het totaal uit 60 vierkanten en kunnen in tal van verschillende vormen neergelegd worden. Bekend is het vierkant van acht bij acht eenheden met een vierkantje in het midden, zoals op onderstaand figuur.

De twaalf stukken zijn allen vernoemd naar een letter, en wel die letter waarop het stuk het meest lijkt. Bij de meeste stukken is dit heel duidelijk, alleen bij de F en de N is wat fantasie nodig.

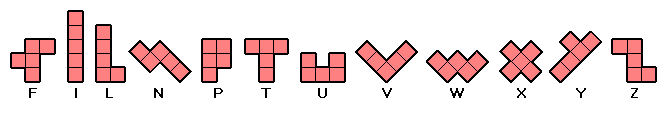
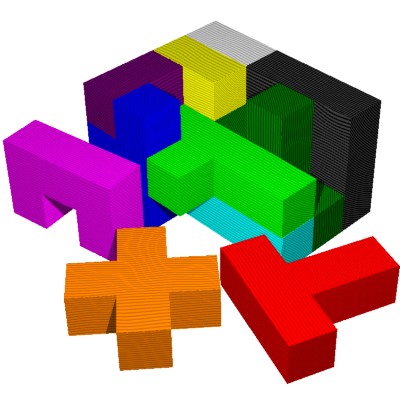
In plaats van platte stukken is een leuke variatie om kubussen te gebruiken. Dan krijg je 12 stukken waarmee bijvoorbeeld een blok te vormen is van 3 x 4 x 5 eenheden. Deze puzzel is in onderstaande figuur weergegeven. Het is niet moeilijk om deze puzzel zelf te maken. Je kan 60 kubussen uit zagen en volgens bovenstaand diagram de twaalf stukken maken. Ook kan je de stukken uit een dikke plank vurenhout zagen. Verf de stukken verschillende kleuren voor een leuk effect.

Met de twaalf stukken kan je verschillende puzzels maken. Er zijn in het totaal 3940 manieren om de stukken in een blok van 3 x 4 x 5 eenheden te passen. Probeer ook de onderstaande figuren na te maken:

               

Een tweede leuke opgave is om alle pentomino stukken na te bouwen. Alle stukken worden dan tweemaal zo groot als het origineel en drie eenheden hoog. De voorbeelden hieronder laten precies zien wat de bedoeling is bij de stukken F, L en Y. Twee stukken kunnen echter niet na gemaakt worden.

               

Er zijn enkele oplossing gegeven van deze puzzels op de website, Er zijn vaak echter veel meer oplossingen mogelijk. Probeer ook zelf vraagstukken te bedenken.