Ontwerp door Peter Query

Ico is gebaseerd op een regelmatig twintigvlak of icosaëder.  Een icosaëder is gemaakt uit twinitg regelmatige driehoeken, heeft twaalf hoeken en dertig ribben. Bij deze puzzel is een zelfde soort verbinding gebruikt als bij de Dodec puzzel. Om deze puzzel te maken moet je dus twintig driehoeken en dertig vliegervormen uitzagen.

Je kan deze puzzel maken door twintig driehoeken en dertig vliegervormen volgens onderstaand diagram uit te zagen. Net als bij de Dodec puzzel wordt hier hout gebruikt van ongeveer 1 tot 1,5 cm dikte. De precieze maten en afmetingen kan je vinden bij de werktekening. Daarna kan je de stukken in elkaar zetten volgens de plaat hierboven.

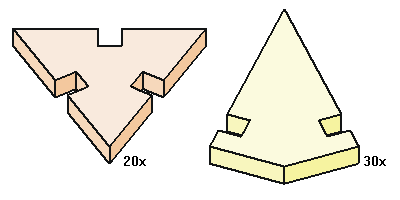
In de bovenstaande diagram zijn alle inkepingen precies even diep, namelijk precies zo diep als het hout dik is. Een varriant hierop is een variabele diepte van de inkeping. Ga je uit van hout met een dikte van 10 eenheden, dan kan je inkepingen van 5, 10 en 15 eenheden diep maken. Eén stuk kan dan ook verschillende inkepingen hebben. Als je alle combinaties van verschillende inkepingen neemt, dan kan je tien verschillende driehoeken en zes verschillende vliegervormen maken. Deze zijn in onderstaand figuur weergegeven.

Uit de bovenstaande figuren kan je twintig driehoeken en dertig vliegervormen kiezen die samen de Ico kunnen vormen. Er zijn tal van combinaties mogelijk met een verschillend aantal mogelijke oplossingen. Een voorbeeld van een dergelijke combinatie zijn alle driehoeken, tweemaal gedupliceerd en de vliegervormen 1-3 twintig maal en 2-2 tien maal. De vraag is nu natuurlijk welke combinaties van driehoeken en vliegervormen de minste oplossingen heeft en daarmee de moeilijkste puzzel geeft.