Regelmaat is een belangrijk begrip bij veelvlakken. Bekend zijn natuurlijk de 'regelmatige' of 'Platonische' veelvlakken. Deze veelvlakken worden als volledig regelmatig beschouwd. De Archimedische en Catalan veelvlakken zijn 'halfregelmatig'. 

Nu is het de vraag hoe die regelmaat bepaald is. Wie of wat bepaald of een veelvlak volledig of halfregelmatig is. Hiervoor wordt vaak gebruik gemaakt van vijf regels. Als aan alle vijf regels voldaan wordt, dan is een veelvlak volledig regelmatig.

1. De zijvlakken zijn regelmatige veelhoeken   

2. De zijvlakken zijn congruent (gelijkvormig)

3. De hoekpunten zijn congruent

4. De standhoeken zijn congruent

5. Het veelvlak is convex

De platonische veelvlakken voldoen aan al deze vijf regels en zijn daarmee volledig regelmatig. Archimedische veelvlakken voldoen aan regels 1, 3 en 5 en zijn daarmee halfregelmatig. De kuboctaëder en icosidodecaëder voldoen daarnaast ook nog aan regel 4 (maar blijven halfregelmatig). Catalan veelvlakken voldoen aan regels 2, 4 en 5. De Rhombische veelvlakken voldoen aan de regels 2, 3, 4 en 5. Catalan en Rhombische veelvlakken zijn dus ook halfregelmatig.

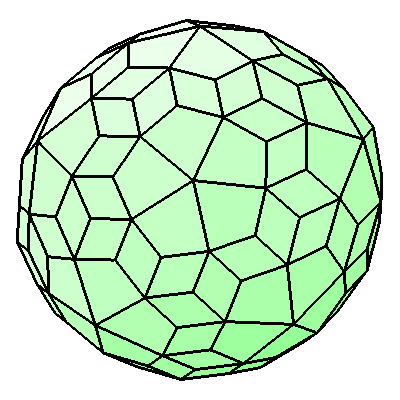
De vijf regels zijn eigenlijk heel beperkt om aan te duiden hoe regelmatig een veelvlak nu eigenlijk is. Als je bijvoorbeeld kijkt naar de rombendeltoïdpentacontahextaëder hieronder, dan is dit een volledig onregelmatig veelvlak: de zijvlakken zijn geen regelmatige veelhoeken, de zijvlakken zijn niet gelijk, de hoekpunten zijn niet gelijk en de standhoeken zijn ook al verschillend. Het enige wat gezegd kan worden is dat het veelvlak convex is. Toch lijkt het veelvlak enige regelmaat te hebben.

Om nu meer inzicht te geven in de exacte regelmaat van een veelvlak, zou ik graag de 'regelmaatindex' willen introduceren. Deze index geeft aan wat de verhouding is tussen het aantal ribben van een veelvlak (een maat voor de omvang) en het aantal herhalingen binnen het veelvlak. Meer informatie over de regelmaatindex is te vinden bij het volgende tabje.