Anders dan bij de vijf regels van regelmaat wordt bij de regelmaatindex gekeken naar het aantal herhalingen binnen een veelvlak. Iets is namelijk meer of minder regelmatig aan de hand van het aantal herhalingen dat te zien is. Binnen een veelvlak zijn er ook herhalingen. Zo kan je een kubus op 24 verschillende manieren neerzetten terwijl deze er precies hetzelfde uit blijft zien. Dit is in onderstaande figuur weergegeven. Een kubus heeft daarmee 24 'posities van gelijkheid'

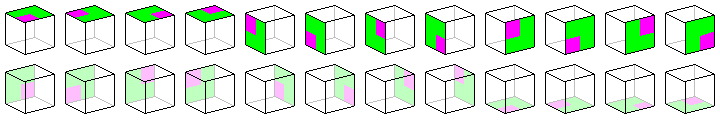
Omdat de octaëder het duale veelvlak van de kubus is, kan je verwachten dat de octaëder ook 24 posities van gelijkheid heeft. Dat dit klopt, kan je in onderstaande figuur zien.

De tetraëder, het kleinste mogelijke veelvlak heeft 'slechts' twaalf posities van gelijkheid. Logisch dat deze piramide er minder heeft dan de octaëder en kubus, want een tetraëder heeft natuurlijk ook minder, vlakken, hoeken en ribben.

Wat hebben deze posities van gelijkheid nu met de regelmaat index te maken? Alles, is hierop het antwoord. Zoals hierboven al aangetoond is, is het aantal posities van gelijkheid niet bij alle veelvlakken gelijk, dit hangt blijkbaar samen met het aantal vlakken/ribben/hoeken van een veelvlak. Hoe meer vlakken/ribben/hoeken, hoe meer posities van gelijkheid er theoretisch mogelijk zijn. 

De regelmaatindex is de verhouding tussen het aantal Posities van gelijkheid (nP) en het aantal ribben (nR). Oftewel in formule:

Voor het aantal ribben is gekozen omdat dit getal beter de complexiteit van een veelvlak aangeeft dan het aantal vlakken en hoekpunten. Bovendien is het aantal ribben afhankelijk van de andere twee, aangezien dit aantal gevormd wordt door de som van het aantal vlakken en hoeken min twee.

De formule voor de regelmaat index kan worden vereenvoudigd geschreven worden door:

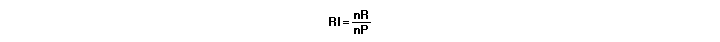
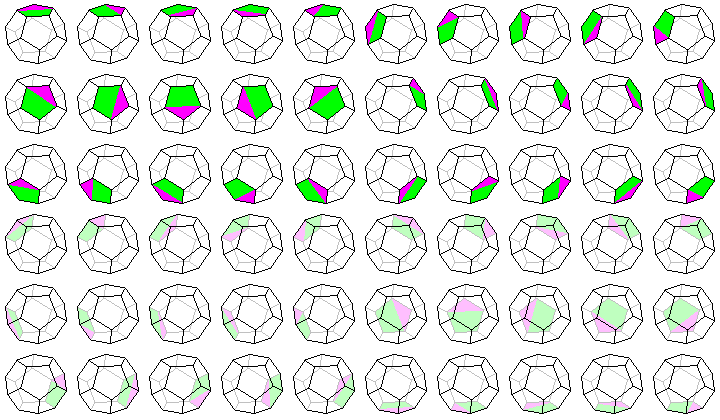
Als je nu kijkt bij een kubus, dan is het aantal posities van gelijkheid 24, het aantal ribben is 12, dus de regelmaatindex (RI) is 0,5. Bij zowel de octaëder als bij de tetraëder blijkt ook de regelmaatindex 0,5 te zijn. Het aantal posities van gelijkheid bij een dodecaëder en icosaëder is 60 (zie figuren hieronder). Beide veelvlakken bezitten 30 ribben en ook deze veelvlakken hebben dus een regelmaatindex van 0,5. Blijkbaar hebben alle Platonische veelvlakken een regelmaatindex van 0,5. Een lagere regelmaatindex is dan ook niet mogelijk.

Hoe hoger de regelmaatindex hoe onregelmatiger het veelvlak. Het maximum van een regelmaatindex wordt begrenst door het aantal ribben. De regelmaatindex kan nooit hoger worden dan het aantal ribben. Bij het tabje voorbeelden kan je van een aantal veelvlakken de regelmaatindex uitrekenen. Duidelijk zal worden dat dit getal veel meer zegt over de regelmaat van een veelvlak dan de vijf regels die eerder zijn geschetst.