Het gebruik van de regelmaatindex zou ik eerst willen demonstreren aan de hand van de halfregelmatige Archimedische en Catalan veelvlakken. Het aantal posities van gelijkheid is erg eenvoudig te bepalen bij deze veelvlakken. Deze is namelijk gelijk aan de bij behorende Platonische veelvlak. Zo heeft de afgeknotte tetraëder twaalf posities van gelijkheid en de afgeknotte kubus of octaëder heeft er 24. 

Het aantal ribben van Archimedische veelvlakken is echter variabel, daarom is het ook te verwachten dat niet alle Archimedische veelvlakken dezelfde regelmaatindex hebben (hoewel ze wel allemaal toto de 'halfregelmatige veelvlakken' behoren). In onderstaande tabel is een samenvatting gegeven van de verschillende Archimedische veelvlakken en hun regelmaatindex

	Veelvlak	nP	nR	RI
	Afgeknotte Tetraëder	12	18	1.5
	Afgeknotte Kubus	24	36	1.5
	Afgeknotte Octaëder	24	36	1.5
	Kuboctaëder	24	24	1
	Rombenkuboctaëder	24	48	2
	Grote Rombenkuboctaëder	24	72	3
	Stompe kubus	24	60	2.5
	Afgeknotte Dodecaëder	60	90	1.5
	Afgeknotte Icosaëder	60	90	1.5
	Icosidodecaëder	60	60	1
	Rombenicosidodecaëder	60	120	2
	Grote Rombenicosidodecaëder	60	180	3
	Stompe dodecaëder	60	150	2.5
	nP=aantal Posities van Gelijkheid
	nR=aantal Ribben
	RI=Regelmaatindex

De regelmaatindex ligt bij de Archimedische veelvlakken dus tussen de 1 en de 3. Dit wil dus zeggen dat de Archimedische veelvlakken niet allemaal even regelmatig zijn. De regelmaatindex geeft dus veel meer specificiteit over de regelmaat van een veelvlak dan enkel de vijf eerder besproken regels. Opmerkelijk is verder dat het afknotten van een veelvlak de regelmaatindex blijkbaar met een factor 3 vergroot (Zo is in feite de grote rombenkuboctaëder een afgeknotte versie van de kuboctaëder, en ook daar klopt deze observatie).

De Catalan veelvlakken zijn de duale tegenhangers van de Archimedische veelvlakken. Verwacht wordt dat de regelmaatindex identiek is aan die van de Archimedische veelvlakken. Je kan zelf ook nagaan dat dit klopt. In onderstaande tabel is een samenvatting gegeven van de regelmaatindex van de Catalan veelvlakken

	Veelvlak	nP	nR	RI
	Triakistetraëder	12	18	1.5
	Triakisoctaëder	24	36	1.5
	Tetrakishexaëder	24	36	1.5
	Rombendodecaëder	24	24	1
	Deltoïdicositetraëder	24	48	2
	Dysdiakisdodecaëder	24	72	3
	Pentagonicositetraëder	24	60	2.5
	Triakisicosaëder	60	90	1.5
	Pentakisdodecaëder	60	90	1.5
	Rombentriakontaëder	60	60	1
	Deltoïdhexakontaëder	60	120	2
	Dysdiakistriakontaëder	60	180	3
	Pentagonhexakontaëder	60	150	2.5
	nP=aantal Posities van Gelijkheid
	nR=aantal Ribben
	RI=Regelmaatindex

Als je kijkt naar andere (halfregelmatige) veelvlakken, dan kan je uitrekenen dat bijvoorbeeld alle prisma's een regelmaatindex van 1,5 hebben, bij alle antiprisma's is de regelmaatindex 2, bij alle dubbelpiramides is de regelmaatindex 1,5 en bij alle trapezoïden is de regelmaatindex ook 2. 

Hieronder nog een voorbeeld voor het berekenen van de regelmaatindex. Alle drie veelvlakken hebben 12 ribben, alle drie de veelvlakken voldoen aan tenminste drie regels van de regelmaat (figuren zijn convex, hoekpunten zijn congruent en de standhoeken zijn congruent). De eerste figuur is een kubus met 24 posities van gelijkheid en dus een regelmaatindex van 0,5. De twee figuur heeft 8 posities van gelijkheid en daarmee een regelmaatindex van 1.5. Het laatste veelvlak heeft een regelmaatindex van 3 doordat het aantal posities van gelijkheid slechts 4 bedraagt.

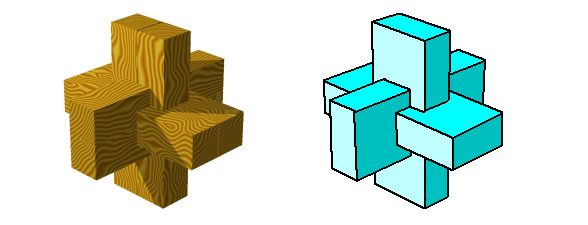
Ook kan je de regelmaatindex van niet-convexe veelvlakken uitrekenen. Zo zal blijken dat de regelmaatindex van de Kepler-Poinsot Veelvlakken ook 0,5 is, net zoals bij de Platonische veelvlakken. Maar ook puzzels, die vaak niet convex zijn hebben een regelmaatindex. Neem bijvoorbeeld de Chinese Kruis Puzzel. Deze puzzel zou beschouwd kunnen worden als een samenstelling van drie rechthoekige balken. In het totaal heeft dit 'veelvlak' dan 36 ribben. Het aantal Posities van Gelijkheid is bij dit veelvlak 12. De regelmaatindex van een Chinese Kruis Puzzel is dan dus 3. 

Nog een laatste voorbeeld is de rombendeltoïdpentacontahectaëder, al reeds aangehaald bij 'de vijf regels' van regelmaat. Dit veelvlak heeft in het totaal 300 ribben. Het aantal posities van gelijkheid is 60. De regelmaatindex is hierbij dus 5, niet eens zo heel veel onregelmatiger dan een Archimedische veelvlak...